ESTEQUIOMETRIA
A estequiometria (ou equações químicas). A palavra vem do grego stoikheion (elemento) e metriā (medida, de metron). A obra Stoichiometria de Nicéforo rendeu muitas linhas nos livros canônicos do Novo Testamento e dos Apócrifos. O termo "estequiométrico" é usado com frequência em Termodinâmica para referir-se à "mistura perfeita" de um combustível e o ar.A estequiometria baseia-se na lei da conservação das massas e na lei das proporções definidas (ou lei da composição constante), e na lei das proporções múltiplas. Em geral, as reações químicas combinam proporções definidas de compostos químicos. Já que a matéria não pode ser criada ou destruída, a quantia de cada elemento deve ser a mesma em antes, durante e após a reação. Por exemplo, a quantia de um elemento A no reagente deve ser igual à quantia do mesmo elemento no produto.
A estequiometria é usada frequentemente para balancear equações químicas. Por exemplo, os dois gases diatômicos hidrogênio e oxigênio podem combinar-se para formar um líquido, água, em uma reação exotérmica, como descrita na Equação [1].
 [1]
[1]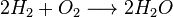 [2]
[2]O termo "estequiometria" também é usado com frequência para as proporções molares de elementos em compostos estequiométricos. Por exemplo, a estequiometria do hidrogênio e do oxigênio na água (H2O) é 2:1. Em compostos estequiométricos, as proporções molares são números inteiros (e é aí que está a lei de proporções múltiplas). Compostos cujas proporções molares não são números inteiros são chamados de compostos não-estequiométricos. A estequiometria não é tão somente usada para balancear equações químicas, mas também para conversões de unidades - por exemplo, de gramas a mols, ou gramas a mililitros. Por exemplo, se temos 2,00 g de NaCl, para achar o número de mols, pode-se fazer o seguinte:


- Quantos gramas de alumínio são necessários para reagir completamente com 85 g de óxido de ferro III?
- Resposta: 28,6875 g de alumínio.
- Num laboratório de química há duas soluções, a primeira é de ácido sulfúrico (H2SO4) com concentração desconhecida, a segunda é de soda cáustica (NaOH) em concentração de 0,10 mol/L. Sabe-se que 25 mL da solução de ácido exigem 22,50 mL da solução de soda cáustica para ser neutralizada completamente. Com base nessas informações, pede-se que se calcule a concentração de ácido na solução.
- Resolução
- Começa-se montando uma regra de 3 simples com base nos dados da solução de soda cáustica:
-
- A 2ª equação será feita com base na reação de neutralização entre o ácido e a base:
- A 2ª equação será feita com base na reação de neutralização entre o ácido e a base:
-
- Com estes dados monta-se uma 3ª equação, em relação à solução ácida:
- Resposta: 0,045 mol/L.
Reagente em excesso e reagente limitante
Nem sempre uma reação ocorre por completo. Isso ocorre, por exemplo, quando um dos reagentes está em excesso e parte dele não reage. O outro reagente, que é consumido primeiro, é denominado reagente limitante.
Geralmente, ao estudar as reações, nós as encaramos como ideais, isto é, encaramos que todos os reagentes reagem completamente; exatamente como é descrito nas equações químicas. No entanto, no mundo real isto nem sempre ocorre. Uma série de fatores pode interferir no desenvolvimento de uma reação química.Por exemplo: há a impureza dos reagentes, seu manejo inadequado, imprecisão das medidas efetuadas pelos aparelhos do laboratório ou máquinas industriais, não completude da reação no momento em as medições são feitas, uma reação concorrente (isto é, que ocorre exatamente ao mesmo tempo em que a nossa reação de interesse pode consumir os reagentes utilizados), a pressão e a temperatura podem variar, e assim por diante.Todos esses fatores devem ser levados em consideração para que se prepare a máxima quantidade de produtos a partir de uma determinada quantidade de reagente. Vamos ver, por exemplo, o que acontece quando a reação não ocorre com o consumo total dos reagentes em razão do excesso de um deles, porque muitas vezes na indústria os reagentes não são colocados em contato nas proporções exatas.Por exemplo, considere a reação abaixo entre o monóxido de carbono e o oxigênio:2 CO (g) + O2 (g) → 2CO2(g)Com base na proporção estequiométrica mostrada na reação balanceada acima, são necessárias duas moléculas de monóxido de carbono para reagir com uma de oxigênio, gerando duas moléculas de dióxido de carbono. A proporção é, portanto, 2 : 1 : 2. Se essa proporção for mudada e um dos reagentes estiver em excesso, a reação não ocorrerá da mesma maneira:2 CO (g) + 2 O2 (g) → 2 CO2(g) + O2 (g)Considerando o exemplo acima, que não está na proporção estequiométrica, verifica-se que o monóxido de carbono é totalmente consumido enquanto que o oxigênio não. Isto significa que o oxigênio é o reagente em excesso e o monóxido de carbono é o reagente limitante.O reagente limitante realmente limita a reação, pois depois que ele é totalmente consumido, a reação cessa, não importando a quantidade em excesso que ainda tenha do outro reagente.Determinação do reagente limitante:A partir da equação química balanceada é possível determinar quem é o reagente limitante e o que está em excesso e a relação entre as quantidades das substâncias envolvidas.Vejamos um exemplo de como realizar este cálculo; consideremos o caso da combustão do álcool:Problema: Uma massa de 138 g álcool etílico (C2H6O) foi posta para queimar com 320g de oxigênio (O2), em condições normais de temperatura e pressão. Qual é a massa de gás carbônico liberado e o excesso de reagente, se houver?
Resolução:
A reação balanceada é dada por:
1 C2H6O(V) + 3 O2(g) → 2CO2(g) + 3H2O(v)
1 mol 3 mol 2 mol
46 g 96g 88g
138g 320g
Só de analisarmos os dados, vemos que a massa de oxigênio é proporcionalmente maior que a do álcool, assim o oxigênio é o reagente em excesso e o álcool etílico é o reagente limitante.
Calculando a massa de gás carbônico formado a partir da quantidade do reagente limitante:
46g de C2H6O ------------88g de CO2
138g de C2H6O ------------x
x = 264 g de CO2
A massa de oxigênio em excesso é determinada de forma análoga:
46g de C2H6O ------------ 96 O2
138g de C2H6O ------------x
x = 288 g de O2
A massa em excesso é a diferença da massa que foi colocada para reagir e a que efetivamente reagiu:320g - 288g= 32 gRendimento
O rendimento diz respeito à quantidade de produto formado, e que foi calculada de acordo com coeficientes.Porém, o resultado obtido da quantidade de produto através da reação, não é o mesmo que se pretendia ao fazer o cálculo, pois o resultado é menor. Desta forma 90% é o rendimento adquirido.Reação de 0º e 1 atm, 11, 2 litros de CO2 com hidroácido de sódio;
Sabendo que o rendimento da reação foi de 90%, qual a massa do carbono de sódio obtido?CO2 + 2NaOH → Na2CO3 + H2O- proporção de quantidade de matéria, coeficientes.1mol de CO2 → 1mol de Na2CO2- regra de três.
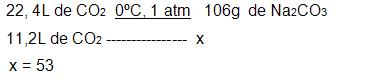 - massa de Na2CO3 com um rendimento de 100%53g- massa de Na2CO3 com um rendimento de 90%
- massa de Na2CO3 com um rendimento de 100%53g- massa de Na2CO3 com um rendimento de 90%
 Tomando como foco de calculo os coeficientes, o rendimento(R) é expresso da seguinte forma:
Tomando como foco de calculo os coeficientes, o rendimento(R) é expresso da seguinte forma:
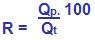
PUREZA
As reações químicas envolvem de forma direta ou indireta percentuais derendimento. Por vezes esperasse pela teoria obter uma determinada quantidade deprodutos, porém no processo experimental essa quantidade não é obtida. Esse fenômenoé bastante comum, já que na teoria não são previstas as perdas ocorridas em processosindustriais. Dessa forma pode-se dizer que quando obtemos valores práticos ouexperimentais iguais aos teóricos a reação teve um rendimento igual a 100%, casocontrário efetuamos uma regra de três para determinar o rendimento da reação de acordocom:Uma amostra de 200g CaCO3 (M=100g), produziu por decomposição térmica 66g deCO2(M=44g/mol), de acordo com a equação, a seguir. Determine o percentual ou grau derendimento para esse processo.CaCO3 → CaO + CO21 mol 1 mol100g---------------------44g200g---------------------- xx = 88g de CO2 – valor teórico – 100% rendimento88g--------100%66g----------- x (grau de rendimento) x = 75% de rendimento
- Com estes dados monta-se uma 3ª equação, em relação à solução ácida:
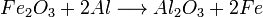




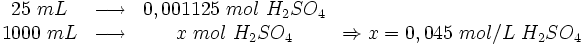
Nenhum comentário:
Postar um comentário